Range of Numeric Values
As we have seen, all numeric types have a range of valid values (p. 41). This range is given by the constants named MAX_VALUE and MIN_VALUE, which are defined in each numeric wrapper type.
The arithmetic operators are overloaded, meaning that the operation of an operator varies depending on the type of its operands. Floating-point arithmetic is performed if any operand of an operator is of floating-point type; otherwise, integer arithmetic is performed.
Values that are out of range or are the results of invalid expressions are handled differently depending on whether integer or floating-point arithmetic is performed.
Integer Arithmetic
Integer arithmetic always returns a value that is in range, except in the case of integer division by zero and remainder by zero, which cause an ArithmeticException (see the later discussion of the division operator / and the remainder operator %). A valid value does not necessarily mean that the result is correct, as demonstrated by the following examples:
int tooBig = Integer.MAX_VALUE + 1; // -2147483648 which is Integer.MIN_VALUE.
int tooSmall = Integer.MIN_VALUE – 1; // 2147483647 which is Integer.MAX_VALUE.
These results should be values that are out of range. However, integer arithmetic wraps around the result if it is out of range; that is, the result is reduced modulo in the range of the result type. To avoid wrapping around out-of-range values, programs should use either explicit checks or a wider type. If the type long were used in the earlier examples, the results would be correct in the long range:
long notTooBig = Integer.MAX_VALUE + 1L; // 2147483648L in range.
long notTooSmall = Integer.MIN_VALUE – 1L; // -2147483649L in range
Floating-Point Arithmetic
Certain floating-point operations result in values that are out of range. Typically, adding or multiplying two very large floating-point numbers can result in an out-of-range value that is represented by infinity (Figure 2.3). Attempting floating-point division by zero also returns infinity. The following examples show how this value is printed as signed infinity:
System.out.println( 4.0 / 0.0); // Prints: Infinity
System.out.println(-4.0 / 0.0); // Prints: -Infinity
Both positive and negative infinity represent overflow to infinity; that is, the value is too large to be represented as a double or float (Figure 2.3). Signed infinity is represented by the named constants POSITIVE_INFINITY and NEGATIVE_INFINITY in the wrapper classes java.lang.Float and java.lang.Double. A value can be compared with these constants to detect overflow.
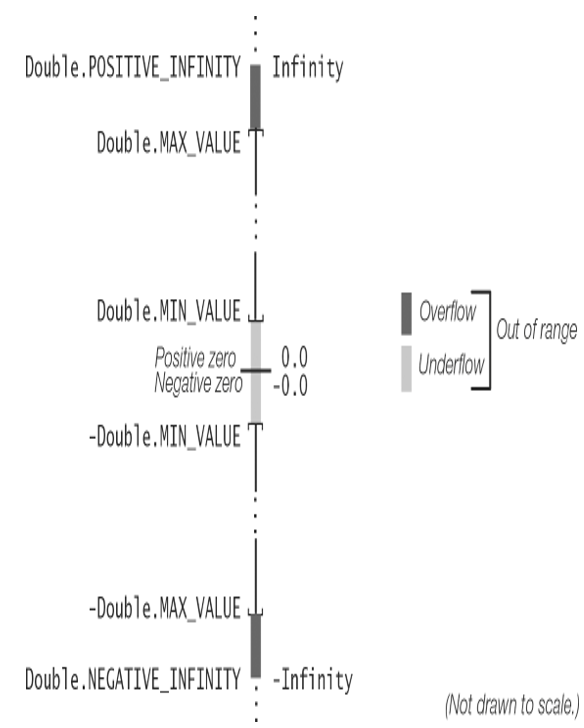
Figure 2.3 Overflow and Underflow in Floating-Point Arithmetic
Floating-point arithmetic can also result in underflow to zero, when the value is too small to be represented as a double or float (Figure 2.3). Underflow occurs in the following situations:
- The result is between Double.MIN_VALUE (or Float.MIN_VALUE) and zero, as with the result of (5.1E-324 – 4.9E-324). Underflow then returns positive zero 0.0 (or 0.0F).
- The result is between -Double.MIN_VALUE (or -Float.MIN_VALUE) and zero, as with the result of (-Double.MIN_VALUE * 1E-1). Underflow then returns negative zero -0.0 (or -0.0F).
Negative zero compares equal to positive zero; in other words, (-0.0 == 0.0) is true.
Certain operations have no mathematical result, and are represented by NaN (Not-a-Number). For example, calculating the square root of –1 results in a NaN. Another example is (floating-point) dividing zero by zero:
System.out.println(0.0 / 0.0); // Prints: NaN
NaN is represented by the constant named NaN in the wrapper classes java.lang.Float and java.lang.Double. Any operation involving NaN produces NaN. Any comparison (except inequality, !=) involving NaN and any other value (including NaN) returns false. An inequality comparison of NaN with another value (including NaN) always returns true. However, the recommended way of checking a value for NaN is to use the static method isNaN() defined in both wrapper classes, java.lang.Float and java.lang.Double.
